Recently Published

Classifying drone RF signals with statistical learning and a small data set
This brief note puts together a couple (non-deep learning) algorithms to classify RF signals using a small open-source data set.This work agrees with Medaiyese, et al. (2021) that large labeled data sets and complicated deep learning may not be essential for classifying drone RF signals.

Population model of UAP sightings
Develops of novel list of UAP 'hot spots,' after using linear regression to control for the overwhelming effects of population density.

Generalized Linear Models: Residuals and Diagnostics
How can we tell if our fitted GLM is consistent with these assumptions, and fits the data at hand adequately?

Document Validation by Simulation: Simulating the Results of a Regression
Gelman and Hill (2006) detail a procedure for validating the results of a regression model by using the fitted coefficients to generate a simulated distribution and compare it to the original y. If the two distributions coincide, it provides evidence that the hypothesized model successfully captures the process that generates y. And if not, it suggests the model is not well-fit.
Below, I generate a simulated dataset, with a Poisson distributed dependent variable, and three independent variables (one of each distribution normal, binomial, and negative binomial). I fit two models, one that accurately describes the simulated data, and another that does not. Then I simulate from both regressions and compare the results to the original y.

Deriving Poisson Regression
This blog examines the mathematics behind Poisson regression for count data. I then create some simulated data, subject it to Poisson regression, and explore R’s functionality.
I cover residuals and residual analysis very briefly, as the next blog will concern those topis for generalized linear models (GLMs) more generally.

Logistic Regression Tutorial
Briefly covers mathematics of logistic regression, then provides a full explanation of R's functionality and interpreting the results

Deriving the Least Squares Solution
Full derivation of the least squares solution for single-variable regression

Modeling Housing Violations in New York City
The purpose of this document is to explore the relationship between 311 calls and housing violations in New York City. After investigating their statistical properties, and incorporating demographic variables, I develop a number of successful models for predicting housing violations in NYC zip codes. After testing each model on a hold-out set, the best model was a special Poisson regression method that accounted for 72 percent of variation in housing violations.
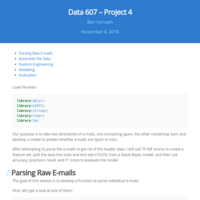
Data 607 – Project 4
Our purpose is to take two directories of e-mails, one containing spam, the other containing ham, and develop a model to predict whether e-mails are spam or ham.
After attempting to parse the e-mails to get rid of the header data, I will use TF-IDF scores to create a feature set, split the data into train and test sets (75/25), train a Naive Bayes model, and then use accuracy, precision, recall, and F1 score to evaluate the model.

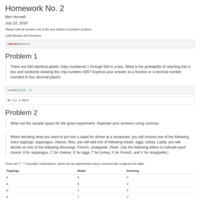
DATA 607—Homework No. 7
An R implementation of the NYT Books API

DATA 607 -- Homework No. 1
Various simple transformations on the UCI repository's mushroom dataset, available at https://archive.ics.uci.edu/ml/datasets/Mushroom/.

Homework Template
Testing to ensure these template settings will carry over to Rpubs correctly